Questions & Approaches
All cellular phenomena are implemented by chemical reactions of diverse molecules with small numbers being encapsulated within a microscopic cellular environment. How should we describe and model stochastic behaviors of the molecules? How can the small number of molecules induce qualitative transition? What kind of thermodynamic law does an equilibrium / non-equilibrium intracellular reaction system follow? We address these fundamental questions and develop methods for their verification using quantitative data.
01.
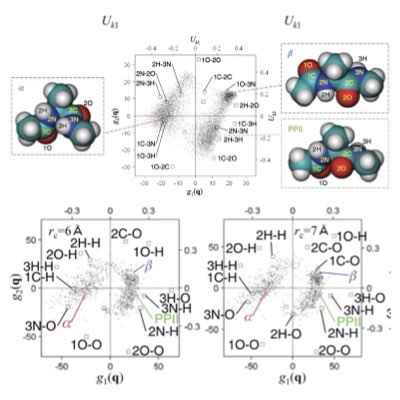
Theory of Chemical Reaction Networks
Intracellular reactions composed of a variety of different molecules and reactions has intrinsic algebraic (circuit) structures. They also operate stochastically, because of the small copy numbers of individual molecules. Theory of chemical reaction networks are indespensable for understanding how robust cellular functions emerge from these diverse yet rare molecues (Learn more: [1], [2]).
02.
Signal Amplification by a Noisy Cascade
A potential constructive role of stochasticity is to bias certain cellular phenomena from the average behaviors. While an averaging effect simply impairs celullar functions in most cases, we have found that stochasticity can substantially amplify an input signal via cascading reactions with a specific network stucture (Learn more).
03.
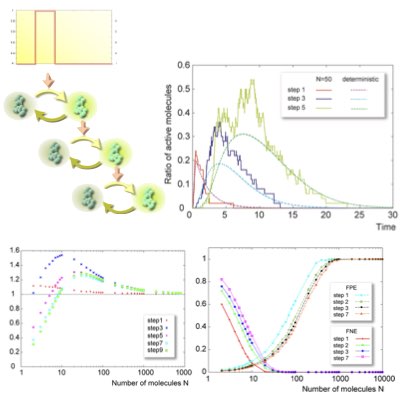
Noise-induced & Discreteness-induced Transitions
In some caces, noise and fluctuation can work as a driving force to induce tranditions in a microscopic system. Noise-induced phenomena may explain why and how biological systems can operate in an ordered manner with noisy & stochastic components. Towards this end, We have discovered a new type of noise-induced transition termed “discreteness-induced transition”, which originates from the discrete nature of inracellular reactions (Learn more).
04.
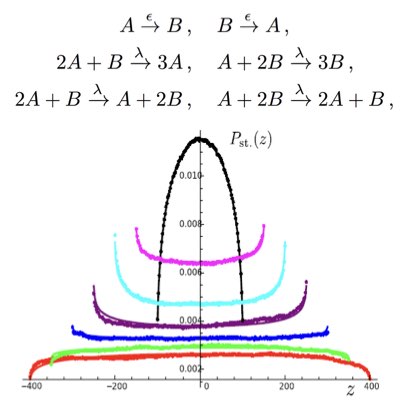
Dissecting & Measuring Noise Sources & Feedback Efficiency
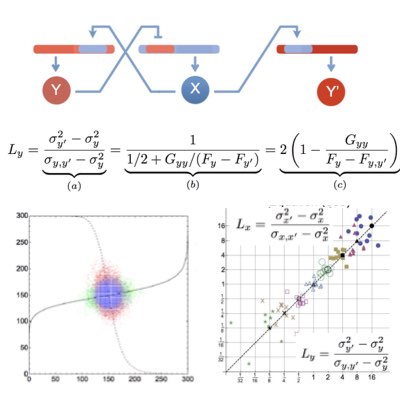
In intracellular networks, individual reactions work concurently as the sources of stochasticity and channels to propagate signals and noise. Understanding the origin of stochasticity in cellular systems requires the development of tactical methods that can appropriately dissect these two different roles of reactions. By extending the dual reporter system introduced by Swain and Elowitz, we proposed a conjugated feedforward and feedback system to estimate feedback efficiency simply based on the statistics of the target and conjugates molecules (Learn more).
05.
Chemical Thermodynamics and Hessian Geometry
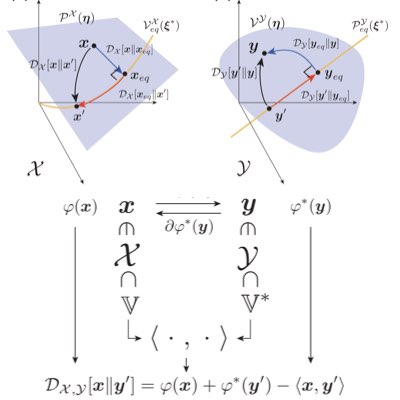
Chemical reaction theory and its thermodynamics are important mathematical bases for describing and analyzing intracellular systems. However, the mathematics that adequately captures the thermodynamic structure of reactive systems, especially their geometrical aspects, has not yet been fully established. We have shown that Hessian geometry, which is utilized in information geometry, is a way to capture the essence of equilibrium thermodynamics of reaction systems. Such a theory is expected to provide a basis for further understanding of non-equilibrium chemical systems (Learn more: [1], [2]).
06.
Information Geometry of Nonequilibrium Thermodynamics
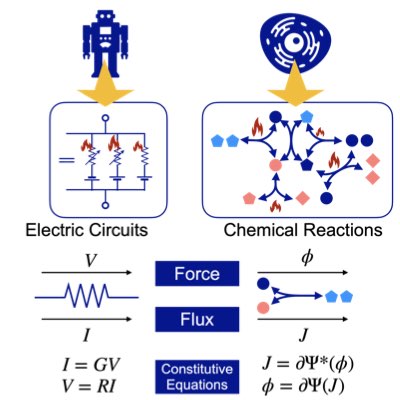
Most chemical reaction systems in living organisms are nonequilibrium. Their nonequilibrium nature is indespensable for producing a variety of biological functions. However, the theory of non-equilibrium reaction networks is not yet well established. We have found that information (Hesse) geometry also plays an essential role in non-equilibrium reaction systems. We are developing a geometric theory of reaction thermodynamics that connects both equilibrium and nonequilibrium chemical thermodynamics (Learn more).
07.
Thermodynamics of Self-Replication
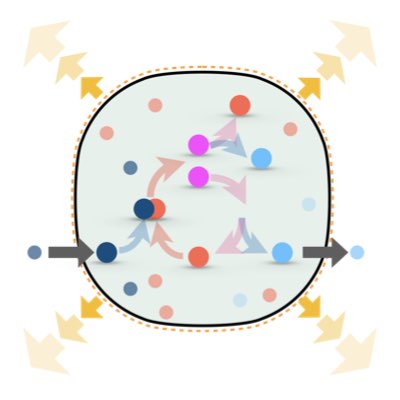
One fundamental difference between non-living and living systems is the ability of self-replication, which can function as a driving force to maintain the non-equilibrium state of living systems. However, it remains unknown as to whether this non-equilibrium state driven by self-replication differs from the typical non-equiriburim state of non-living systems sustained by flow of material or energy. We address this problem by establishing the thermodynamics of growing reaction systems in which self-replication and volume change are conjugated(Learn more).
08.
Delay & Stability of Genetic & Synthetic Switches
Delay is another ubiquitous phenomenon in intracellular networks, which can drastically change the stability of the networks depending on their structures. We clarified that the asympototic behaviours of genetic networks only consisting of positive feedback loops cannot be altered by any delay in the network, which provides a sufficient condition to construct stable genetic switches. We also proposed a method to design stable synthetic switche by extending a simple abstract network with required stability to more complicated networks (Learn more).
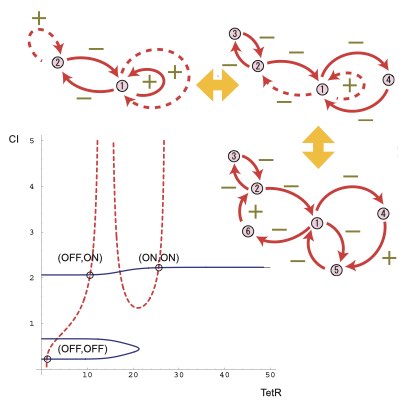
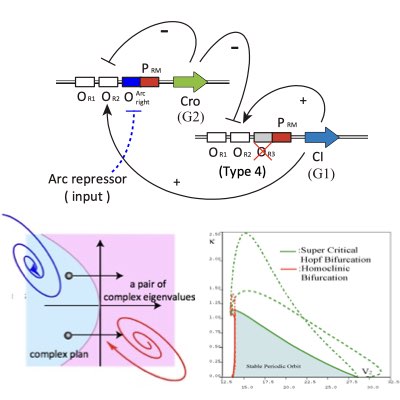
09.
Designing Synthetic Oscillators
Oscillation is a dynamic component of living systems to coordinate and synchronize different intracellular processes. Thus, the design and control of oscillatory dynamics in a cell is relevant for modulating the global states of the cell. By employing the bifurcation theory, we proposed a method for the design of robust synthetic oscillators using genetic networks.
10.
Inducing Large Conformational Changes of Proteins
The conformational structure of a protein and its fluctuations are the key determinants of its functionality. Therefore, the reasonable control and design of a structure are fundamental for molecular engineering. However, it is still elusive how we should measure the difference of protein structure for this purpose and how we can induce large structural changes under that measure. In this work, we propose using Kullback Leibler divergence of conformational fluctuation as a standardized measure of structural differences. By exploiting an underlying information-theoretic structure, we proposed a method to predict the optimal perturbation that can induce the largest change of conformational fluctuations to a protein (Learn more: [1], [2]).