Theory for Biological Information Processing
How do living systems explore, process, & exploit information Learn MoreQuestions & Approaches
Living systems collect and process information related to the environment in order to exert an appropriate response (movement, state change, etc.). However, However, it remains unclear as to how a living system recognizes and processes information with stochastic and noisy microscopic molecular components. To clarify the mechanism, we are working on construction of a mathematical theory of dynamic environmental recognition/searching, and information-thermodynamics of cellular information processing.
01.
Noisy Signal Processisng by Cells
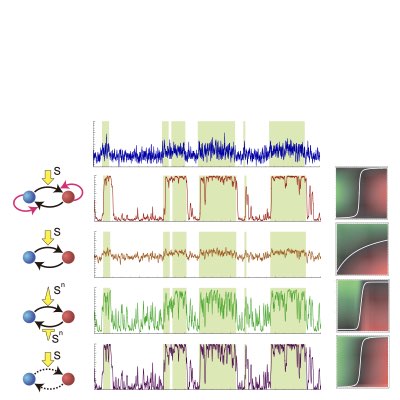
Sensing the environment through noisy receptors inevitably impairs the information transferred into a cell. Nonetheless, in some cases, a cell can still respond quite faithfully to a dynamic change in the environmental state, which suggests that the cell is able to extract relevant information of the environment from a noisy signal. Using the theory for sequential Bayesian inference, we have derived the optimal dynamical network to decode a dichotomous change in the environment from a noisy receptor output, which can be implemented by an auto-regulatory phosphorylation and dephosphorylation cycle (Learn more: [1], [2]).
02.
Tug-of-war with Reinforcement Implements Bayesian Computation
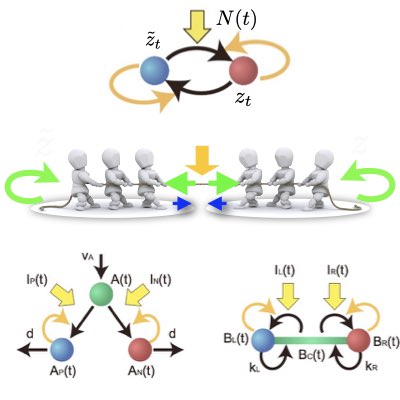
The fundamental dynamical property for implementing Bayesian decoding from a noisy signal has been demonstrated to reflect a reinforced tug-of-war between two alternative hypotheses (the environmental state is either on or off) that is biased by the noisy signal. By exploiting this interpretation, we have shown that the Bayesian decoding can be implemented by networks other than the auto-regulatory cycle, such as auto-regulatory branching differentiation and polarization(Learn more: [1], [2]).
03.
Bayesian Computation & Noise-induced Transition
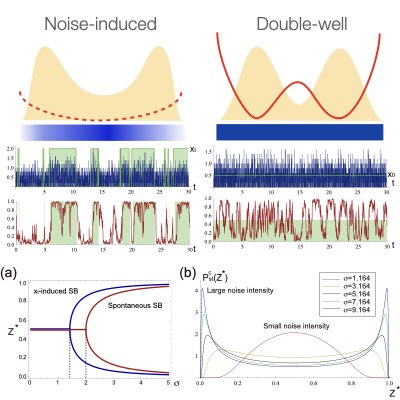
Decoding information from a noisy signal requires balancing an insensitivity to noise with sensitivity to the change in the environment. How can an auto-regulatory cycle or the reinforced tug-of-war achieve these contradictory propertires? We found that the noise-induced transition is the underlying dynamical mechanism necessary for balancing these two requirements. Moreover, we proposed a method to identify the noise-induced behaviour in the networks.(Learn more: [1], [2])
04.
Processing Dynamic and Noisy Information
Actual environmental changes are not only dichotomous but have further layers of complexity. By extending the approach of sequential Bayesian computation, we derived several relaction networks relevant to the chemotaxis of bacteria and amoebic cells, in which both temporal and spatial sensing of the environmental state coexist.
05.
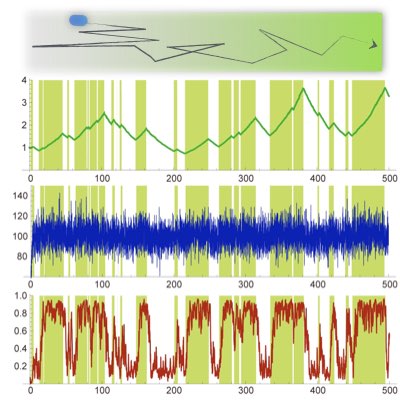
Optimality of Bacterial Chemotactic System
Does the optimal information processing mechanism as derived above really exist in real organisms? We have found that the standard biophysical model of E. coli chemotactic network agrees perfectly with the equations derived by the optimal filter. In addition, the feedback function of methylation, which had been measured experimentally, was reproduced by the theoretical prediction of the optimal filter. This result suggests that cellular information processing has an optimal structure.(Learn more).
06.
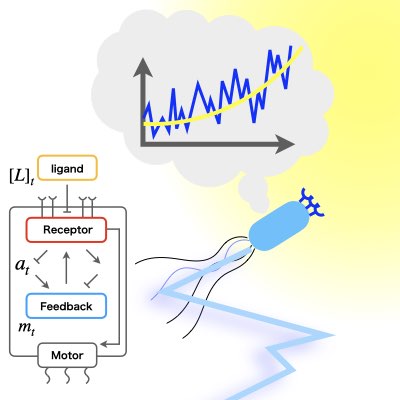
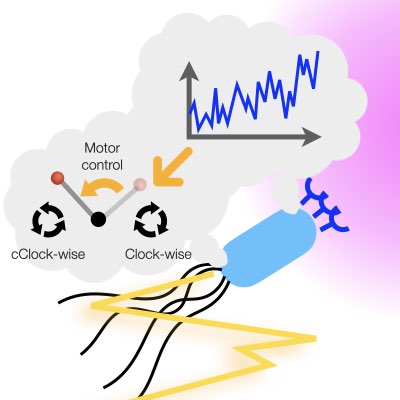
Optimal Sensing and Control of Chemotactic Systems
The organism not only senses information in the environment, but also uses that information to control its own motion and explore the environment. The control mechanisms of living organisms are highly noisy and nonlinear, making them difficult to analyze by widely used linear control theory. We have developed a theory that can handle run-tumble chemotaxis of the organism by combining partially observable optimal control theory and Kullback-Leibler control. Such a theory is expected to provide a theoretical basis for dealing with the optimality of various types of biological detection mechanisms. (Learn more).
07.
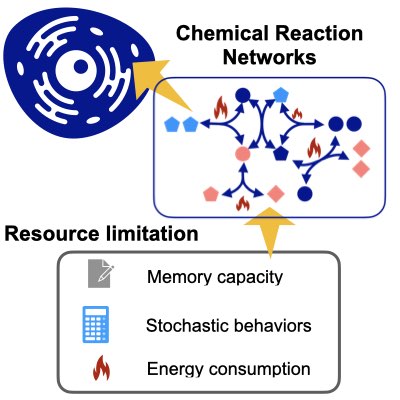
Optimal inference & Control with Resource Limitation
Biological systems realize a variety of information processing and control with extremely limited memory and stochastically behaving elements. However, we lack an appropriate theory to deal with such constraints over inference and control. Using mathematical techniques from mean-field control, we have developed a new theory that can take into account the memory capacity and uncertain behavior of the controller. By utilizing and developing this theory, we may be able to handle various problems such as transitions in information processing strategies depending on changes in available resources (Learn more:[1],[2]).
08.
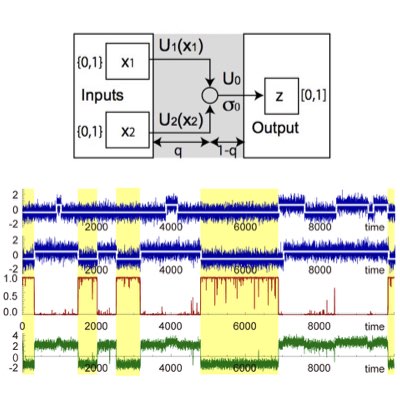
Bayesian Gates for Logical Operations in the Face of Noise
Recent requirements for down-sizing and low-operational energy of modern computer architectures highlight the importance of implementing robust computational systems that can operate under quite noisy situations. Motivated by the works conducted on noisy information processing by cells, we proposed an idea for implementing noise-immune logical operations by the Bayesian computation at the level of physical implementation of the logic gates. Our work suggests the importance of adopting Bayesian logic not only at the higher layers of computation, but also at the lower layers (Learn more).