Questions & Approaches
Living systems have the ability to flexibly adapt to a stochastically changing environment. Diversification of phenotypic or genetic states in a population is a Darwinian mechanism by which living systems increase their chance of survival in the face of a sudden environmental change. In contrast, living organisms have also developed certain machinery to allow for a short-term survival response, such as the human brain, which can choose a better phenotypic states by sensing and predicting the future environment. By employing the underlying information-theoretic structures shared by both Darwinian selection and predictive adaptation, we are trying to establish an integrative theory for these different adaptation strategies.
01.
Biased Intrinsic Dynamics by Selection
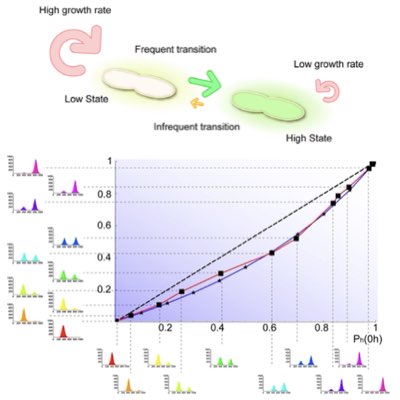
The stochastic dynamics of intracellular reactions can introduce phenotypic diversity in a genetically heterogeneous population. However, the diversity of the population does not always reflect the intrinsic properties of the underlying stochastic reaction, especially when the phenotypic differences are subject to selection. By combining an experimental measurement and a theoretical model, we have shown that the intrinsic dynamics of a synthetic toggle switch, i.e., its stability, is substantially biased by selection at the population level. This result highlights the discrepancy between the single cell-level and population-level behaviours of cells under selection (Learn more).
02.
Thermodynamic Variational Structure in Population Dynamics
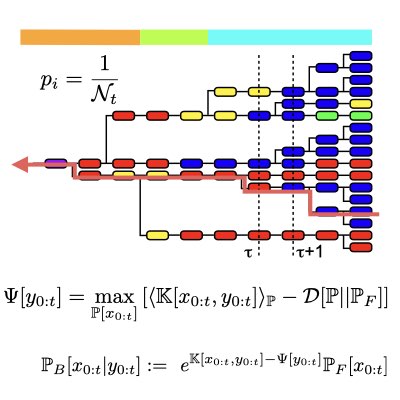
The relationship between behaviours at the single-cell and the population levels had long-been mathematically elusive. By introducing a path-integral formulation into classic population dynamics, we found that the impact of selection can be captured by the difference between the prospective time-forward path probability and the retrospective time-backward probability, which characterize single-cell and population behaviours, respectively. Moreover, we identified a variational structure in the population dynamics at the path level, which is mathematically equivalent to the structures underlying thermodynamis, Bayesian inference, and information theory (Learn more and more).
03.
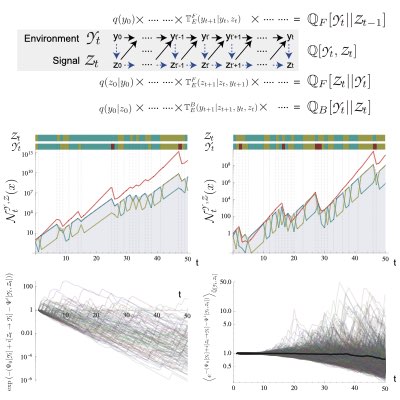
Natural Selection as Information Processing
The common variational structure between population dynamics and information theory enabled us to interpret adaptation via Darwinian selection as a type of information processing. Specifically, we found that selection can be regarded as an form of information compression, similar to the rate distortion, at the level of the retrospective path probability. This result provides us an information-theoretical basis by which to integrate adaptation by Darwinian selection with predictive adaptation via sensing and prediction. Through this approach, we obtained very general relations between sensing information and the fitness gain achieved by using the information received(Learn more: [1], [2]).
04.
Fluctuation Relations of Fitness and Information
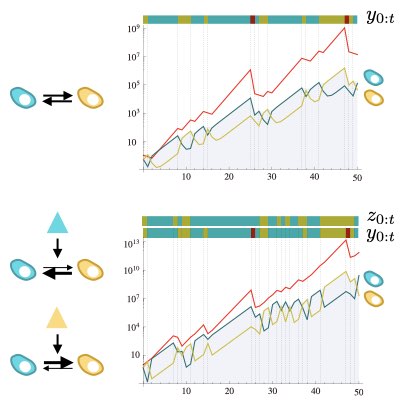
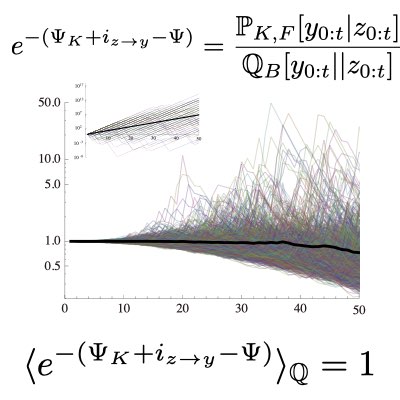
The retrospective time-backward path probability plays a very similar role to the path probability of the time-reversal trajectories in stochastic thermodynamics. Using this connection, we found that fluctuation relations can hold for fitness in a stochastically changing environment and for information obtained by sensing the environment. From an evolutionary biology viewpoint, the fluctuation relations for fitness and information generalize the notion of an evolutionary stable strategy (ESS) in a changing environment, and indicate that there always exist suboptimal strategies that can invade the ESS on average by exploiting rare fluctuations of the environment(Learn more and more).
05.
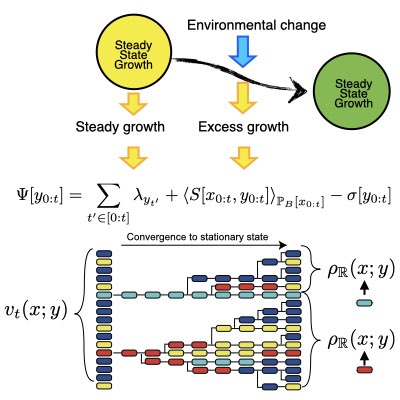
Housekeeping and Excess Fitnesses
The actual growth of a heterogeneous population is strongly dependent on the actual realization of the environment. Controling population dynamics by external manipulation of the environmental states requires understanding the response of the population, especially that of fitness, to specific external perturbations. Based on the path-integral formulation of population dynamics, we dissected the fitness of a population into house-keeping (ie.e, the stationary growth condition) and excess (i.e., growth induced by environmental change) components. Based on the mathematical connection with steady-state thermodynamics, we have shown that a Clausius-like inequality can holds for the excess fitness when the underlying single-cell behaviour satisfies the detailed balance condition. Our results also highlight the importance of non-equiriburim nature of intrinsic dynamics in individual cells to achieve controllability of the population (Learn more).
06.
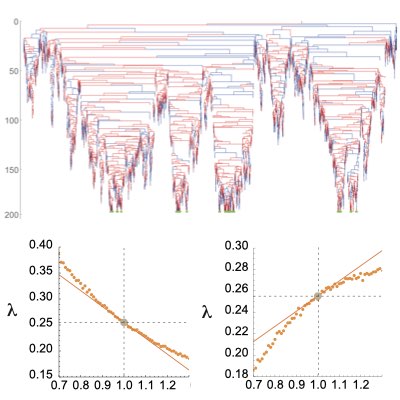
Branching Process & Fitness Response Relation
The characterization of time-forward and time-backward dynamics in path integral representations of population dynamics is strongly related to branching and ancestral processes. We combine the theory of semi-Markov processes with the path representation of continuous-time multi-type age-structured branching processes, and relate it to the large deviation theory. As an application, we have developed a method for predicting the fitness response from a cell lineage tree. Such a method can work as a basis for predicting the direction of population dynamics from data. (Learn more).
07.
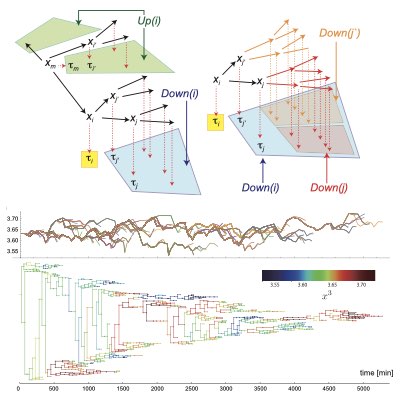
Inference of Cellular States from Cellular Lineage Trees
The dynamics of cell proliferation strongly depends on the phenotypic as well as genotypic state of individual cells. Information on the fraction of phenotypes in a population and its dynamics is essential for predicting population dynamics and drug responses. However, it is generally difficult to measure such phenotypic states. We have developed a method to infer the phenotypic state of a cell based on the nature of the proliferation dynamics of individual cells in the measured genealogical information. Our method (Lineage EM algorithm) can estimate the hidden (unobserved) phenotypic state from a measured lineage tree data. Using this method, we have identified a slow dynamic component that vary across generation time of E. coli populations. We believe that our results will provide a basis for cellular lineage data analysis. (Learn more).
08.
Fitness Value of Individual Information Processing
Many organisms adapt to various environments as a population through natural selection. At the same time, they also have mechanisms by which individual cells or organisms actively sense the environment to behave adaptively as individuals. How much fitness value do such individual information processing mechanisms have? By extending the fluctuation theorem of fitness and information, we have shown that the fitness value of individual information processing can exceed the amount of information obtained by the information processing. We believe that this result is the first step toward a unified understanding of the relationship between individual and polulation adaptation. (Learn more).
09.
Relation btween Natural Selection & Individual Learning
Evolution is a process of adaptation at the population level through the generation of novel mutations and their selection. On the other hand, many living systems show adaptation as individuals by learning from their own experiences or those of their ancestors and by changing their behavior. We have developed a theory that integrates populational evolution and individual learning. Using this theory, we have shown that ancestral learning, which is learning from ancestral information, essentially accelerates evolution, and we have proposed an extended version of Fisher's fundamental theorem that quantitatively analyzes the relationship between evolution and learning. These methods lead to a further understanding of learning and evolution. (Learn more).
10.
Integrating Neuroscience & Evolutionary Biology
Neuroscience and evolutionary biology, two of the major disciplines in biological research, have essentially developed independently, although they both have a common aim of understanding the mechanisms of biological adaptations. Thus, we envision that integration of these two fields may lead to gaining a deeper understanding of how biological systems balance the two strategies of adaptations, predictive and evolutionary adaptations, during the process of evolution.