Our Projects
Goal, Methods, Targets, & ApproachesUnderstanding Biological Information Processing
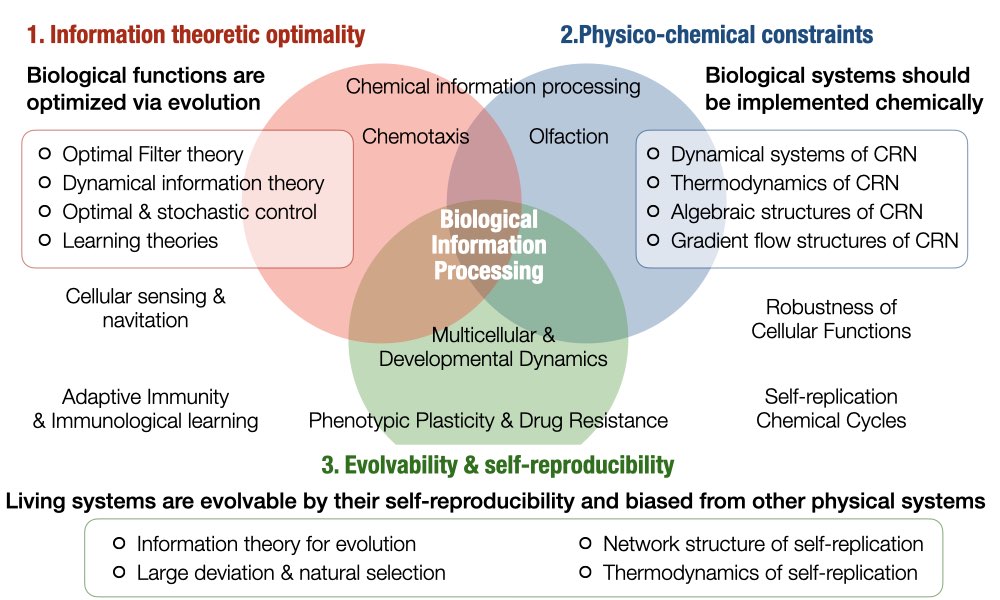
In order to understand biological information processing systems created by evolution, we focus on their (1) information theoretic optimality, (2) physico-chemical constraints, and (3) evolvability & self-reproducibility. To grasp such aspects, we are working on
- construction of relevant mathematical theories (Learn More)
- development of informatic methods (Learn More)
- analysis of various biological phenomena (Learn More)
Mathematics
In order to describe and understand information processing in living organisms, mathematical methods and theories that can capture the essence of the phenomena are necessary. While many theories and techniques have already been developed in the fields of mathematical science, physics, and engineering, they are rarely applicable to biological phenomena as they are. We need to modify, improve, and in some cases, recreate them for our purpose. Specifically, we are using the following theories in our works:
Dynamical Systems(DS)
- Deterministic & stochastic DS
- Deterministic bifurcation theory
- Stochastic bifurcation theory
- Gradient flow
Stochastic Processes
- Point processes
- Diffusion processes
- Conditoned stochastic processes
- Large deviation theory
Information Theory
- Dynamic information theory
- Optimal filtering theory
- Sequential decision theory
- Information geometry
Thermodynamics
- Chemical thermodynamics
- Stochastic thermodynamics
- Information thermodynamics
- Thermodynamics of evolution
Control & Learning Theories
- Optimal control theory
- Stochastic control theory
- Statistical learning theory
- Reinforcement learning
Algebra & Homology
- Algebraic graph thoery
- Algebraic homology
- Algebraic geometry
- Group & symmetry
Informatics
Quantitative measurement techniques for biological phenomena have made great strides in the past two decades, providing us with the data we need to investigate phenomena in detail and to test theories. We are also developing a variety of informatics methods to extract appropriate information from these quantitative data and integrate them with theories:
Image Analysis
- 3D segmentation of mammalian embryos
- 4D tracking of embryonic developmental process
- GUI development for 4D data
Statistical Analysis
- Inference & prediction of population dynamics equation
- Inference & prediction of histry-dependent point processes
- Inference & prediction of information flow in networks
Bioinformatics
- Hidden state inference of cellular lineage trees
- Machine learning of T-cell receptor repertoires
- Machine learning of Raman-Omics correspondance
Numerical Simulations
- Simulation of deterministic & stochastic equations
- Simulation of multi-cellular developmental processes
- Simulation of immunological learning processes
Analysis of Biological Phnomena
A close examination of biological systems let us find that even seemingly simple single cells possess breath-takingly sophisticated and efficient functions. Toward understand information processing in cells, we are working on the mathematical understanding of various phenomena in collaboration with our collaborators: